Binary search is a quick pursuit calculation with run-time intricacy of Ο(log n). This inquiry calculation takes a shot at the standard of partition and overcome. For this calculation to work appropriately, the information assortment ought to be in the arranged structure.
Binary search searches for a specific thing by contrasting the center most thing of the assortment. In the event that a match happens, at that point the list of thing is returned. On the off chance that the center thing is more prominent than the thing, at that point the thing is looked in the sub-cluster to one side of the center thing. Something else, the thing is looked for in the sub-cluster to one side of the center thing. This cycle proceeds on the sub-exhibit also until the size of the sub-cluster lessens to zero.
Working
For a binary search to work, it is compulsory for the objective cluster to be arranged. We will get familiar with the cycle of twofold pursuit with a pictorial model. Coming up next is our arranged cluster and let us expect that we have to look through the area of significant value 31 utilizing twofold pursuit.

First, we shall determine half of the array by using this formula −
mid = low + (high – low) / 2
Here it is, 0 + (9 – 0) / 2 = 4 (integer value of 4.5). So, 4 is the mid of the array.

Now we compare the value stored at location 4, with the value being searched, i.e. 31. We find that the value at location 4 is 27, which is not a match. As the value is greater than 27 and we have a sorted array, so we also know that the target value must be in the upper portion of the array.

We change our low to mid + 1 and find the new mid value again.
low = mid + 1
mid = low + (high – low) / 2
Our new mid is 7 now. We compare the value stored at location 7 with our target value 31.
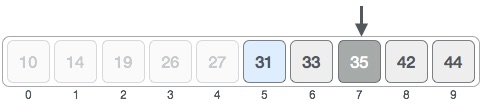
The value stored at location 7 is not a match, rather it is more than what we are looking for. So, the value must be in the lower part from this location.

Hence, we calculate the mid again. This time it is 5.
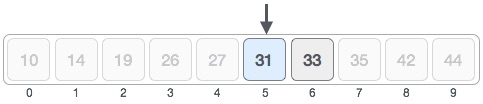
We compare the value stored at location 5 with our target value. We find that it is a match.

We conclude that the target value 31 is stored at location 5.
Binary search halves the searchable items and thus reduces the count of comparisons to be made to very less numbers.
Pseudocode