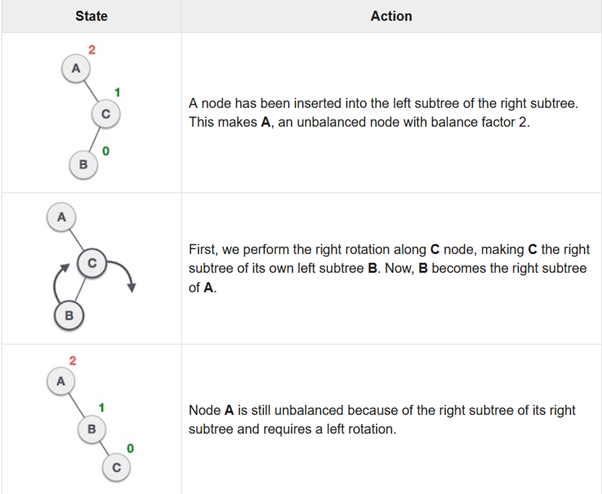
Named after their inventor Adelson, Velski & Landis, AVL trees are height balancing binary search tree. AVL tree checks the height of the left and the right sub-trees and assures that the difference is not more than 1. This difference is called the Balance Factor.
Here we see that the first tree is balanced and the next two trees are not balanced −

In the second tree, the left subtree of C has height 2 and the right subtree has height 0, so the difference is 2. In the third tree, the right subtree of A has height 2 and the left is missing, so it is 0, and the difference is 2 again. AVL tree permits difference (balance factor) to be only 1.
Balance Factor = height(left-subtree) − height(right-subtree)
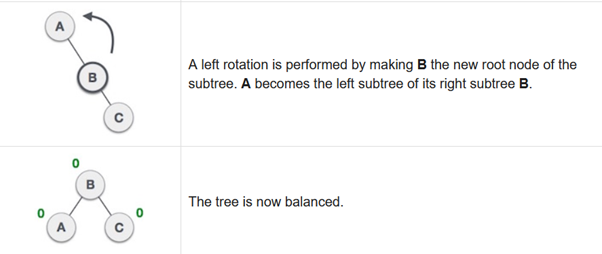
If the difference in the height of left and right sub-trees is more than 1, the tree is balanced using some rotation techniques.
AVL Rotations
To balance itself, an AVL tree may perform the following four kinds of rotations −
- Left rotation
- Right rotation
- Left-Right rotation
- Right-Left rotation
The first two rotations are single rotations and the next two rotations are double rotations. To have an unbalanced tree, we at least need a tree of height 2. With this simple tree, let’s understand them one by one.
Left Rotation
If a tree becomes unbalanced, when a node is inserted into the right subtree of the right subtree, then we perform a single left rotation –
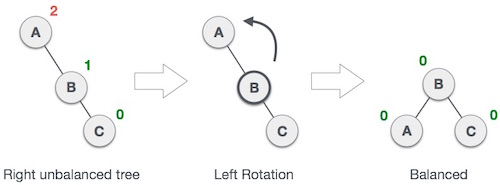
In our example, node A has become unbalanced as a node is inserted in the right subtree of A’s right subtree. We perform the left rotation by making A the left-subtree of B.
Right Rotation
AVL tree may become unbalanced, if a node is inserted in the left subtree of the left subtree. The tree then needs a right rotation.
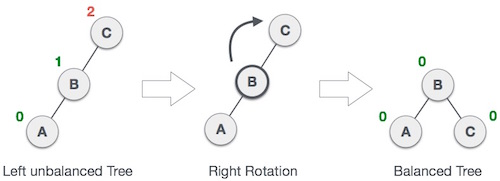
As depicted, the unbalanced node becomes the right child of its left child by performing a right rotation.
Left-Right Rotation
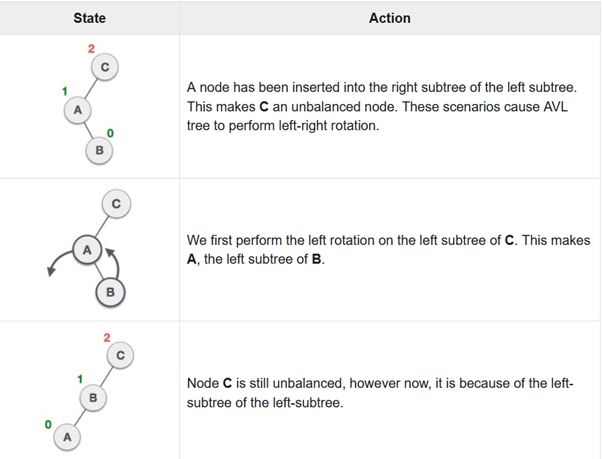
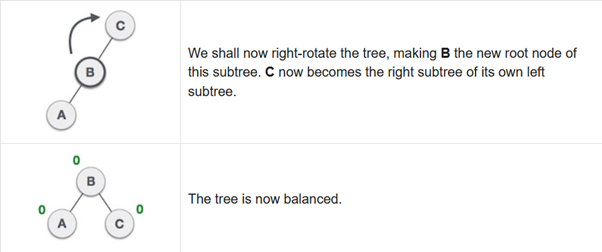
Right-Left Rotation
The second type of double rotation is Right-Left Rotation. It is a combination of right rotation followed by left rotation.